Integral ∫√(x²–9) / x³ dx

Integral de \(\frac{\sqrt{x^2 - 9}}{x^3}\): Desarrollo Completo

Paso 1: Elección de la sustitución

Para eliminar la raíz cuadrada \(\sqrt{x^2 - 9}\), usamos:

\( x = 3\sec\theta \) ⇒ \( dx = 3\sec\theta\tan\theta\,d\theta \)

Justificación: La expresión \(x^2 - 9\) sugiere una identidad trigonométrica donde \( \sec^2\theta - 1 = \tan^2\theta \).

Paso 2: Reescribir la integral

Sustituimos \(x\) y \(dx\) en la integral original:

\[ \int \frac{\sqrt{(3\sec\theta)^2 - 9}}{(3\sec\theta)^3} \cdot 3\sec\theta\tan\theta\,d\theta \]

Desarrollo algebraico:

\[ = \int \frac{\sqrt{9\sec^2\theta - 9}}{27\sec^3\theta} \cdot 3\sec\theta\tan\theta\,d\theta \] \[ = \int \frac{3\sqrt{\sec^2\theta - 1}}{27\sec^3\theta} \cdot 3\sec\theta\tan\theta\,d\theta \]

Paso 3: Aplicar identidad trigonométrica

Usamos \( \sqrt{\sec^2\theta - 1} = \tan\theta \):

\[ = \int \frac{3\tan\theta}{27\sec^3\theta} \cdot 3\sec\theta\tan\theta\,d\theta \]

Simplificación paso a paso:

\[ = \frac{9}{27} \int \frac{\tan^2\theta \cdot \sec\theta}{\sec^3\theta}\,d\theta \] \[ = \frac{1}{3} \int \frac{\tan^2\theta}{\sec^2\theta}\,d\theta \] \[ = \frac{1}{3} \int \sin^2\theta\,d\theta \quad (\text{porque } \tan^2\theta/\sec^2\theta = \sin^2\theta) \]

Paso 4: Integrar \(\sin^2\theta\)

Usamos la identidad del ángulo mitad:

\[ \sin^2\theta = \frac{1 - \cos 2\theta}{2} \]

Integramos término a término:

\[ \frac{1}{3} \int \frac{1 - \cos 2\theta}{2}\,d\theta = \frac{1}{6} \int 1\,d\theta - \frac{1}{6} \int \cos 2\theta\,d\theta \] \[ = \frac{1}{6}\theta - \frac{1}{12}\sin 2\theta + C \]

Paso 5: Regreso a la variable \(x\)

De \(x = 3\sec\theta\):

\[ \sec\theta = \frac{x}{3} \quad ⇒ \quad \cos\theta = \frac{3}{x} \quad ⇒ \quad \theta = \arccos\left(\frac{3}{x}\right) \]

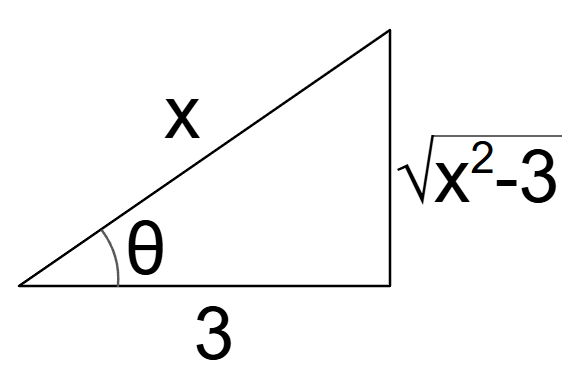
Triángulo de referencia:
- Hipotenusa: \(x\)
- Adyacente: \(3\)
- Opuesto: \(\sqrt{x^2 - 9}\)

Cálculo de \(\sin 2\theta\):

\[ \sin\theta = \frac{\sqrt{x^2 - 9}}{x}, \quad \cos\theta = \frac{3}{x} \] \[ \sin 2\theta = 2\sin\theta\cos\theta = 2\left(\frac{\sqrt{x^2 - 9}}{x}\right)\left(\frac{3}{x}\right) = \frac{6\sqrt{x^2 - 9}}{x^2} \]

Resultado Final

\[ \boxed{ \frac{1}{6} \arccos\left(\frac{3}{x}\right) - \frac{\sqrt{x^2 - 9}}{2x^2} + C } \]